TCS Codevita | Hermoine Number

In this blog, we will discuss the problem asked in TCS Codevita 2019.

Before running into the solution please try it by yourself first.

Problem Description:

Voldemort is finally dead, Hermoine is bored and has now developed some interest in mathematics, so she keeps challenging her friends. Harry is now one of the victims of those hard problems and needs your help to solve this puzzle.

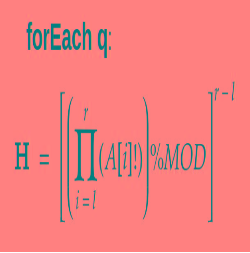
She calls the result to be Hermoine Number H.

Since H can be large, you need to print the result modulo MOD = 1000000007

Constraints:

N <= 10^5

A[I] <= 10^5

Input Format:

The first, line provides an integer N denoting the number of elements in Array A

Second-line provides N space-separated values for the array A,

Thrid-line provides an integer denoting Query (q) corresponding the problem statement

Next q lines contain two numbers l, r denoting the values mentioned above in the statement

Output:

q lines containing the value of H mod 1000000007

Explanation:

Example 1:

Input:

5
1 2 3 4 5
2
2 2 
2 4

Output:

1
82944

Example 2:

Input:

10
77883 4860 68269 31574 57351 20528 45398 54148 37399 31382
10
5 9
2 8
2 9
6 6
1 3
1 9
7 8
6 10
2 7
1 2

Output:

667891964
31641898
769678014
1
29992112
654285930
654285930
776096678
444042335
886182048
728170986

---

Implementation using C++:

#include <bits/stdc++.h>
using namespace std;
#define ll long long int
#define MOD 1000000007
ll fact[100005];
int main()
{
    fact[0] = 1;
    fact[1] = 1;
    for (int i = 1; i < 100005; i++)
    {
        fact[i] = (fact[i - 1] * i) % MOD;
    }
    ll n;
    cin >> n;
    vector<ll> a;
    ll temp;
    for (ll i = 0; i < n; i++)
    {
        cin >> temp;
        a.push_back(temp);
    }
    ll q;
    cin >> q;
    while (q--)
    {
        ll l, r;
        cin >> l >> r;
        ll mul = 1;
        for (ll i = l; i <= r; i++)
        {
            mul = (mul * fact[a[i-1]]) % MOD;
        }

        ll ans = 1;
        for (ll i = 0; i < r - l; i++)
        {
            ans = (ans * mul) % MOD;
        }
        cout << ans <<endl;
    }
    return 0;
}

---

We have done this solution in the easiest way possible, So share and support us for more blogs like this.

Happy Coding!

Follow us on Instagram @programmersdoor

Join us on Telegram @programmersdoor

Please write comments if you find any bug in the above code/algorithm, or find other ways to solve the same problem.

Follow Programmers Door for more.

#blog #interview #placement #learn #computer #science