top of page
Search

Root Finding Techniques | Secant Method

In this article, we will be going to study the Secant method in numerical analysis and design using Python.
 

Algorithm


  • Read a,b,E

  • Compute f(a) and f(b)

  • for i=1 to n in steps of 1 do

  • m=af(b)-bf(a)/f(b)-f(a)

  • if(|f(m)|<E) then

  • a=b and b=m

  • endif

  • else

  • Write does not converge a,b,f(a),f(b)

  • endfor

  • Write convergent solution m,f(m)

  • stop

 

Flowchart


 

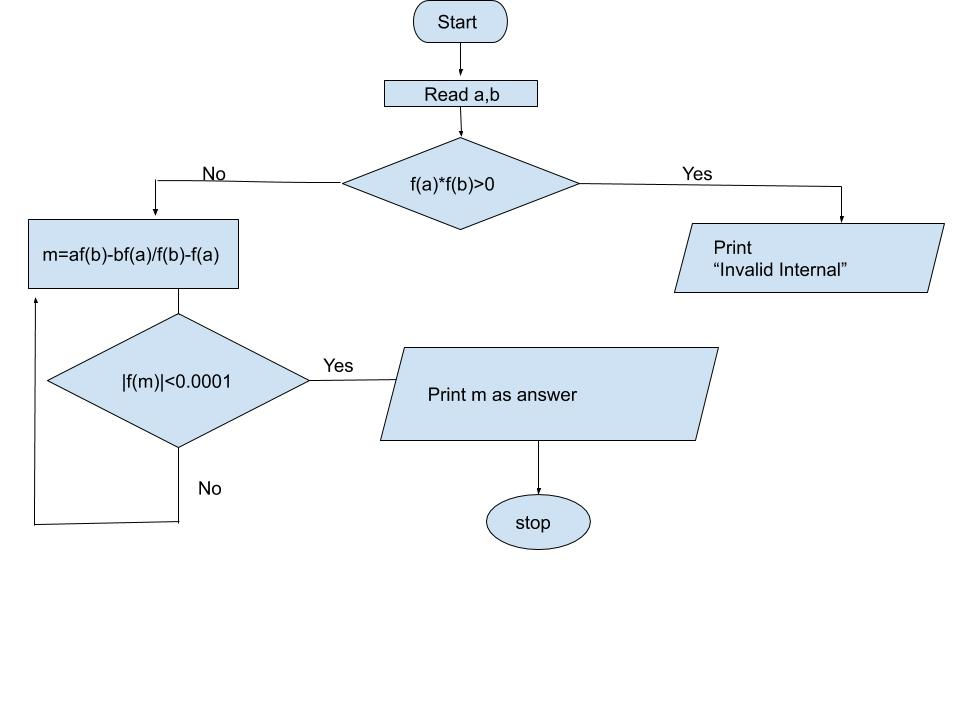
Program


import math
def f(x): 
    return x*x*x - x -1
   

def secant(a,b): 
  
    if (f(a) * f(b) <0.0):
        while True:
            m=(a*f(b)-b*f(a))/(f(b)-f(a))
            a=b
            b=m

            if (abs(f(m)) < 0.0001):
                break 
        print("Root",round(m,4))
    else:
        print("Cannot find roots")

a =1.0
b = 2.0
secant(a, b)
 

Example


Q]Find the real root of the equation x^3-x-1=0 by secant method up to 4 decimal places?


Solution-

F(x)=x^3-x-1
To find x0 and x1 
F(0)=-1 , F(1)=-1 , F(2)= 5
 
Root[1,2]
F(1.5)=0.875 , F(1.4)=0.343 , F(1.3)= -0.103
 
Changing x0= 1.3 and x1= 1.4
 F(x0)= -0.103 and F(x1)= 1.323042
 
(First case) x2=x0*F(x1)-x1*F(x0) =1.323042
 F(x1)-F(x0)
  F(x2)= -0.007136
 
(Second case)  x3=x1*F(x2)-x2*F(x1) =1.323605
 F(x2)-F(x1)
 F(x2)= -0.000481
 
(Third case) x4=x2*F(x3)-x3*F(x2) =1.324717
 F(x3)-F(x2)
 F(x2)= -0.000004
Hence the correct answer(root) up to 4 decimal places is x=1.3247
 

Happy Coding!

Follow us on Instagram @programmersdoor

Join us on Telegram @programmersdoor


Please write comments if you find any bug in the above code, or want some updates.

Follow Programmers Door for more.

 
 
 

Comments

bottom of page