.png)
In this blog, we will deep dive into Graphs. So bear with us till the last 😊
Introduction to Graphs
A graph is a data structure (V, E) that is a collection of nodes that have data and are connected to other nodes:
A finite set of vertices V also called nodes.
A collection of edges E represented as ordered pairs of vertices (u,v)
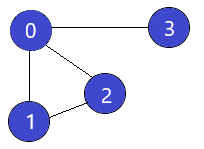
V = {0, 1, 2, 3}
E = {(0,1), (0, 2), (1,2), (0,3)}
G = {V, E}Let's try to understand this through an example. On Facebook, everything is a node. That includes User, Photo, Album, Event, Group, Page, Comment, Story, Video, Link, Note...anything that has data is a node.
Graphs Terminology:
Adjacency: A vertex is said to be adjacent to another vertex if there is an edge connecting them. Vertices 2 and 3 are not adjacent because there is no edge between them.
Path: A sequence of edges that allows you to go from vertex A to vertex B is called a path. 0-1, 1-2, and 0-2 are paths from vertex 0 to vertex 2.
Directed Graph: A graph in which an edge (u,v) doesn't necessarily mean that there is an edge (v, u) as well. The edges in such a graph are represented by arrows to show the direction of the edge.
Undirected Graphs: Undirected graphs are such graphs in which the edges are bi-directional or in other words directionless. That is, if there is an edge between vertices u and v then it means we can use the edge to go from both u to v and v to u.
Graph Representation:
Graphs are commonly represented in two ways:
Adjacency Matrix
Adjacency List
Let us look at each one of the above two methods in details:
Adjacency matrix:
It is a 2D array of V x V vertices. Each row and column represent a vertex.
If the value of any element a [ i ][ j ] is 1, it represents that there is an edge connecting vertex i and vertex j.
The adjacency matrix for the undirected graph is always symmetric.
Adjacency Matrix is also used to represent weighted graphs.
If adj [ i ][ j ] = w, then there is an edge from vertex i to vertex j with weight w.
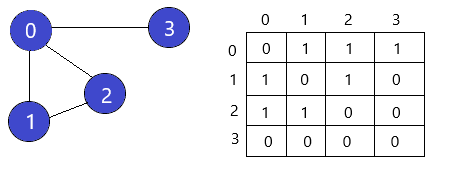
Since it is an undirected graph, for edge (0,2), we also need to mark edge (2,0); making the adjacency matrix symmetric about the diagonal.
Pros: Representation is easier to implement and follow. Removing an edge takes O(1) time.
Cons: Consumes more space O(V^2). Even if the graph is sparse, it consumes the same space. Adding a vertex is O(V^2) time.
Adjacency List:
It represents a graph as an array of linked lists.
The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
An adjacency list is efficient in terms of storage because we only need to store the values for the edges.
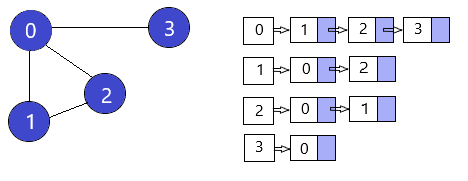
Pros: Saves space O(|V|+|E|). In the worst case, there can be C(V, 2) number of edges in a graph thus consuming O(V^2) space. Adding a vertex is easier.
Cons: Queries like whether there is an edge from vertex u to vertex v are not efficient and can be done O(V).
Happy Coding!
Follow us on Instagram @programmersdoor
Join us on Telegram @programmersdoor
Please write comments if you find any bug in the above code/algorithm, or find other ways to solve the same problem.
Follow Programmers Door for more.
Comments